Is there any bias whatsoever in modern hash function outputs?

Question

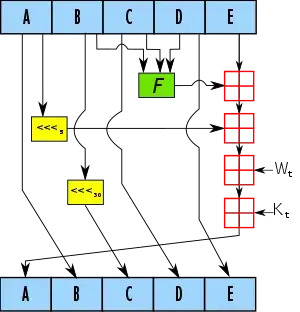
The following is a representative example of a common hash function:-

The asymmetry is clear, and I would expect additional edge effects in the A and E output words. So I'd be surprised if the probability distributions between words A to E are identical to the nth degree. The same asymmetric construction argument clearly applies to all other hash architectures.

In general cryptography and as NIST does, it's common to treat a bias $\epsilon < 2^{-64}$ as negligible. So an $\epsilon$ is expected of some degree as our constructions are imperfect.

The question therefore is: is there any estimate of the theoretical bias across the block width of hash function outputs? Assume the limiting case of an infinite number of hash inputs. Would the output probability distributions be (say for the above example) $P_{\infty}(A) = P_{\infty}(B) = P_{\infty}(C) = P_{\infty}(D) = P_{\infty}(E)$ exactly, and $\epsilon = 0.0$?

I won't be accepting the current answer as that deals with empirical measures, but I'm asking about theoretical expectations. There is no computationally bounded adversary. I'm just curious.

---

NB. I take "bias" to mean the standard NIST definition (SP 800-90B) as "A random process (or the output produced by such a process) is said to be biased with respect to an assumed discrete set of potential outcomes (i.e., possible output values) if some of those outcomes have a greater probability of occurring than do others."

I'm really not sure if Is any group of bits in a SHA-1 hash more/less unique than another? is similar or not.

Answer 1

If there were any detectable bias, I wouldn't be posting about it on a forum of pseudonymous wackos like me on the internet—I would be getting top billing (or beaking, as the case may be) in a top-tier cryptography conference, and the champagne would be popping, and Twitter would be abuzz with speculation, and Hacker News would be extra insufferable.

Specifically, with the exception of 2-pass Snefru[1][2], no major hash function with advertised preimage and collision resistance has ever seen its preimage resistance broken[3] (archive). (Yes, there's a paper that everyone and their dog cites on an MD5 preimage attack[4], but it's not cheaper than the best generic attack[5].)

---

_{P.S. The formula $\epsilon = 2^{-(s n - k)/2}$ appears to be a quotation from an ID Quantique marketing whitepaper with a garbled definition which Paul read out of context to draw a nonsense conclusion in the self-accepted answer of his own that he cited.}