Difference between SHA 512, SHA 512 Half, SHA 256

Question

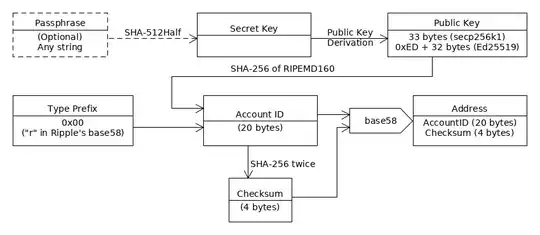
I was trying to create a python wrapper for RIPPLE crypto currency, and i ran into SHA 512 half which i have no idea or reverse googled it to no avail. Can someone help me understand the difference. Currently i am assuming its any 256 bits of SHA512. RIPPLE Address Encoding

Answer 1

SHA-256 is a function with up to $2^{64}$ bits of input, which are broken into 512-bit blocks, and with a 256-bit output. It is conjectured to be collision-, preimage-, and second-preimage resistant at (resp.) 128-, 256-, and 256-bit security levels, but it has the unfortunate property that given $\operatorname{SHA-256}(m)$ but not $m$, it is relatively easy to compute $\operatorname{SHA-256}(m \mathbin\Vert p \mathbin\Vert m')$ for an arbitrary suffix $m'$, where $p$ depends only on the length of $m$.

SHA-512 is a function with up to $2^{128}$ bits of input, which are broken into 1024-bit blocks, and with a 512-bit output. It is conjectured to be collision-, preimage-, and second-preimage resistant at (resp.) 256-, 512-, and 512-bit security levels, but it has the unfortunate property that given $\operatorname{SHA-512}(m)$ but not $m$, it is relatively easy to compute $\operatorname{SHA-512}(m \mathbin\Vert p \mathbin\Vert m')$ for an arbitrary suffix $m'$, where $p$ depends only on the length of $m$.

‘SHA-512half’ is probably SHA-512 truncated to 256 bits. Thus it takes up to $2^{128}$ bits of input, broken into 512-bit blocks, and yields a 256-bit output. Like SHA-256, it is conjectured to be collision-, preimage-, and second-preimage resistant at (resp.) 128-, 256-, and 256-bit security levels. Unlike SHA-256 or SHA-512, to compute $\operatorname{SHA-512half}(m \mathbin\Vert m')$ for any $m'$ (whether with the padding $p$ or not) given only $\operatorname{SHA-512half}(m)$ and not $m$, it is conjectured to cost at least an expected $2^{255}$ SHA-512 computations.

The functions SHA-256 and SHA-512 resemble independent uniform random choices of function, except for the length extension property, whereas SHA-512 and SHA-512half are obviously not independent since SHA-512half is just half the output of SHA-512 on the same input. SHA-512/256 is like SHA-512half, except it it uses different initialization vectors and thus resembles another independent uniform random choice of function.