3

I have limited math's knowledge so sorry if this question sounds stupid.

I saw many people complaining about AES, Twofish and Serpent that these ciphers all could be crackable in the near future and even today with big datacenters. But all these ciphers use max. 256 bit keys . And because there is no better way of finding the key then brute force the ciphers are equally strong.

Would it be possible to take these algorithms e.g AES and just change the key size from 256 to 512 or 1024? I mean the algorithm is well tested, you would just have to modify the key and block size.

Maarten Bodewes
  • 96,351
  • 14
  • 169
  • 323
Richard R. Matthews
  • 4,545
  • 9
  • 31
  • 49

4 Answers4

13

I saw many people complainig about AES , twofish and serpent that these ciphers all could be crackable in the near future and even today with big datacenters .

This is a good example of why we should always ask for citations and explanations, rather then just accepting what people say at face value with no scrutiny. These claims are about as far from reality as possible.

But all these ciphers use max. 256 bit keys . And because there is no better way of finding the key then bruteforce the ciphers are equally strong .

These 3 ciphers all have similar if not identical parameter configurations because they were all designed for the AES competition. It is true enough for practical purposes (but not exactly so) that all three are equally strong and that the only way you'll break them without side channel attacks is via brute force.

Which is to say that you won't break them, at all.

Would it be possibel to take these algos e.g AES and just change the key size from 256 to 512 or 1024 ?

It is not possible to just increase the key size for an algorithm like AES; There are other aspects that are derived from the size of the key that you would have to take into account and modify as well. For instance, the AES key schedule (which is part of the AES block cipher) of AES-128 and AES-256 differs.

I mean the algo is well tested , you would just have to modify the key and blocksize .

Ok, let's concede and say we construct such a thing, and also assume we don't somehow introduce additional points of failure while doing so: What problem have we solved by increasing the key/blocksize? It was already impossible to search. Perhaps this is a good question to ask those people that were complaining about how easy it is to break AES, twofish, and serpent...

Why can't we give block ciphers bigger keys

We can, we do not need to. You can always construct make an algorithm use more space and time. The goal is to use the least amount of resources possible to get the job done. Once you understand this, it will be clear why we do not use massive keys or hundreds of cipher rounds.

Maarten Bodewes
  • 96,351
  • 14
  • 169
  • 323
Ella Rose
  • 19,971
  • 6
  • 56
  • 103
10

I saw many people complainig about AES , twofish and serpent that these ciphers all could be crackable in the near future and even today with big datacenters

Let me go through some of the lesser known details about the NSA's capabilities, and how fast they are able to break AES-256:

  • Their annual budget has been drastically underreported; it is actually $100 trillion dollars per year (that is, the world-wide GDP), and has been at that level for the past 100 years.

  • They spend all that money on AES-cracking equipment (and so, yes, the spooks are working for free)

  • They purchase AES-breaking chips for $0.01 (that is, one cent) each (hey, volume discount); each chip has a billion AES engines on it, and each engine can test one trillion AES keys per second.

Hence, given their investment, they can test $100 \text{ trillion} \times 100 / 0.01 \times 1 \text{ billion} \times 1 \text{ trillion} = 10^{39}$ keys per second.

They are now trying to break their first AES-256 key; they expect success in around $2^{255} / 10^{39} = 5.7E+37$ seconds, or in approximately $10^{20}$ times the current age of the universe. I'm not sure what that key is, or how relevant it will be after the heat death of the universe, but I'm sure it's pretty critical...

poncho
  • 154,064
  • 12
  • 239
  • 382
8

Cryptographers can and we do create block ciphers with bigger keys, take for instance the Threefish cipher which has key/block sizes of 256, 512 and 1024 bits.

However, since strong block ciphers with a key of 256 bits cannot be cracked even when quantum computers come of age, there is no need to use them for a cipher. Instead they are used for special purposes such as the use in a hash algorithm. That would of course be Skein - a SHA-3 finalist- for the Threefish algorithm.

The statement that "these ciphers all could be crackable in the near future and even today with big data centers" is completely wrong. People that complain about the key size for that reason don't know what they are talking about.

It is often not all that easy to change the key size. The algorithm may well depend on the key size for the key schedule, for instance. But mainly we don't because there isn't a need to when it comes to implementing ciphers. And for hash algorithms other parameters need to be changed as well, such as the block size and tweak for Skein.

Maarten Bodewes
  • 96,351
  • 14
  • 169
  • 323
6

Respondents have well addressed the futility of trying to brute force a 256 bit AES key. It's hard. But I want to focus on your last paragraph.

Would it be possible to take these algorithms e.g AES and just change the key size from 256 to 512 or 1024? I mean the algorithm is well tested, you would just have to modify the key and block size.

Actually, no you can't. AES is well tested and a number of people have studied it. It works as a fait accompli by virtue of having been designed as a cohesive unit, with all sub operations working perfectly together. This is AES:-

AES

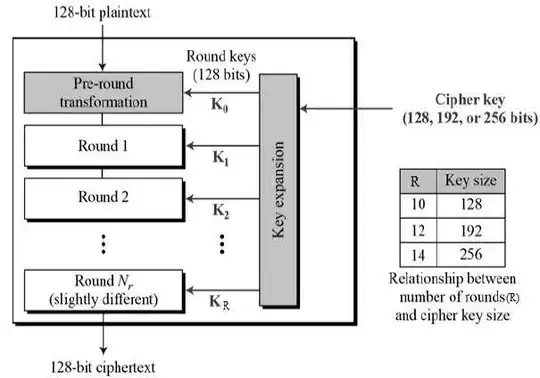
The rounds and the key expansion are the clever bits. A key of predetermined length is expanded so that derivatives of it can be introduced at each round in the algorithm. The key expansion is carefully designed to maximise entropy, avoid weak states and collisions. And they don't repeat so all round keys will be different. The algorithm is proven to work for 10 /128, 12 /192 and 14 /256 round /key permutations. And they also all produce fixed width (128 bit) round keys which contributes to having a 128 bit block width. That's invariant.

If you decide to upgrade AES to a 768 bit block width for uber security, you can't realistically. How would you expand a key of some length to produce repeated but different round keys of 768 bit width? The key scheduling is one of the most important parts of a cipher. It would mean a complete rewrite of the key scheduler.

And the individual round algorithm would have to be expanded to 768 bits. The following isn't from AES, but it has beautiful symmetry and illustrates to difficulty of arbitrary block width expansion:-

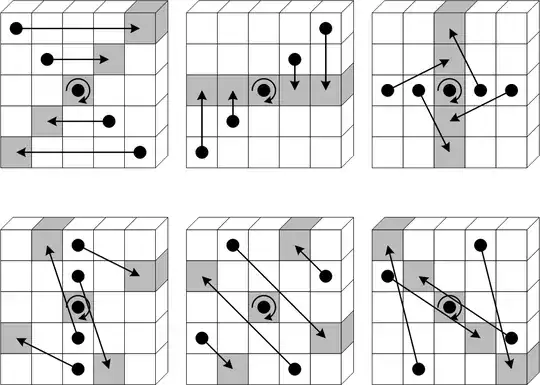
Keccard

Imagine this table containing all the bits in a round. It's 5 x 5 bits, and you can see the careful way the bits cycle round symmetrically. This adds to diffusion and the avalanche effect. Now imagine adding another row to create a 5 x 6 table. For a start, there's no middle bit in an even number of bits. You'd need to completely redesign the bit permutation sequence.

All the words above are a long winded way of saying that if you tried upgrading AES or any other cryptographic primitive, you'd have to completely rewrite it from scratch. So it's no longer well tested and you're back at square one.

Paul Uszak
  • 15,905
  • 2
  • 32
  • 83