And if I am on the right track, how do I reach the solution from here?
I'm doing a CS game and I've hit a wall (I'm a rank beginner when it comes to encryption) on the encryption portion. I've been given the encrypted output and what I think (from my research) is an encoded version of the key using this:
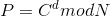
For me, C is what I'm looking for, d = 7, N = 98286183916580532129117891164396375520832348985166654489180704043300879122347 and P = 89511674269883781051088511817946305647658886680759682801944853433540569894936.
p and q for N are 294156383975755063828794349953398256143 and 334129018681034197306379539716603659429
C was created randomly and is known to be 16 bytes. P is known because it was the first 32 bytes of the encrypted file (that I ripped out using a hex editor and turned into base 10) and d and N were both hardcoded.
I tried reversing it manually (using modular arithmetic, since a = b mod n then b = a mod n so C = root7(PmodN) ) but I got a 37 byte number that I know must be incorrect. Can someone please tell me where I'm going wrong?
I can post the source if it's necessary.