Is calculating a hash code for a large file in parallel less secure than doing it sequentially?

Question

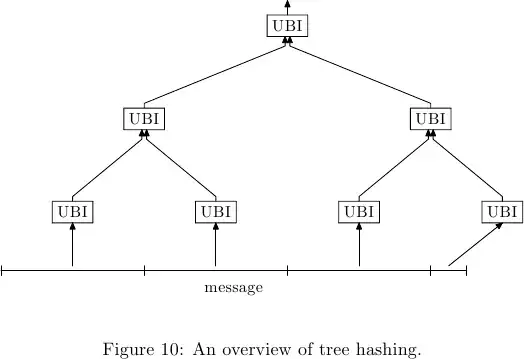
I would like to improve the performance of hashing large files, say for example in the tens of gigabytes in size.

Normally, you sequentially hash the bytes of the files using a hash function (say, for example SHA-256, although I will most likely use Skein, so hashing will be slower when compared to the time it takes to read the file from a [fast] SSD). Let's call this Method 1.

The idea is to hash multiple 1 MB blocks of the file in parallel on 8 CPUs and then hash the concatenated hashes into a single final hash. Let's call this Method 2, show below:

---

---

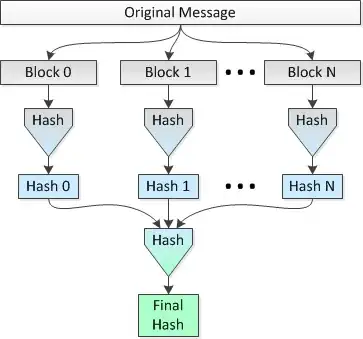
I would like to know if this idea is sound and how much "security" is lost (in terms of collisions being more probable) vs doing a single hash over the span of the entire file.

For example:

Let's use the SHA-256 variant of SHA-2 and set the file size to 2^35=34,359,738,368 bytes. Therefore, using a simple single pass (Method 1), I would get a 256-bit hash for the entire file.

Compare this with:

Using the parallel hashing (i.e., Method 2), I would break the file into 32,768 blocks of 1 MB, hash those blocks using SHA-256 into 32,768 hashes of 256 bits (32 bytes), concatenate the hashes and do a final hash of the resultant concatenated 1,048,576 byte data set to get my final 256-bit hash for the entire file.

Is Method 2 any less secure than Method 1, in terms of collisions being more possible and/or probable? Perhaps I should rephrase this question as: Does Method 2 make it easier for an attacker to create a file that hashes to the same hash value as the original file, except of course for the trivial fact that a brute force attack would be cheaper since the hash can be calculated in parallel on N cpus?

Update: I have just discovered that my construction in Method 2 is very similar to the notion of a hash list. However the Wikipedia article referenced by the link in the preceding sentence does not go into detail about a hash list's superiority or inferiority with regard to the chance of collisions as compared to Method 1, a plain old hashing of the file, when only the top hash of the hash list is used.

Answer 1

If you want to use Skein (one of the SHA-3 candidates) anyway: it has a "mode of operation" (configuration variant) for tree hashing, which works just like your method 2.

It does this internally of the operation, as multiple calls of UBI on the individual blocks. This is described in section 3.5.6 of the Skein specification paper (version 1.3).

You will need a leaf-size of 1 MB (so, Y_l = 14, for the 512-bit variant, 15 for 256, 13 for 1024) and a maximum tree height Y_m = 2 for your application. (The image shows an example with Y_m >= 3.)

The paper does not really include any cryptographic analysis of the tree hashing mode, but the fact that it is included (and even mentioned as a possible use for password hashing) seems to mean that the authors consider it at least as save as the "standard" sequential mode. (It is also not mentioned at all in the proof paper.)

---

On a more theoretical level:
Most ways of finding collisions in hash functions rely on finding a collision in the underlying compression function f : S × M -> S (which maps a previous state together with a block of data to the new state).

A collision here is one of these:

• a pair of messages and a state such that f(s, m1) = f(s, m2)
• a pair of two states, a message block, so that f(s1, m) = f(s2, m)
• a pair of messages and a pair of states such that f(s1, m1) = f(s2, m2).

The first one is the easiest one to exploit - simply modify one block of your message, and let all the other blocks same.

To use the other ones, we additionally need a preimage attack on the compression function for the previous blocks, which is usually thought to be even more complicated.

If we have a collision of this first type, we can exploit it in the tree version just as well as in the sequential version, namely on the lowest level. For creating collisions on the higher levels, we again need preimage attacks on the lower levels.

So, as long as the hash function (and its compression function) is preimage resistant, the tree version has not more collision weak points than the "long stream" one.

Answer 2

Actually a tree-based hashing as you describe it (your method 2) somewhat lowers resistance to second preimages.

For a hash function with a $n$-bit output, we expect resistance to:

• collisions up to $2^{n/2}$ effort,
• second preimages up to $2^{n/2}$,
• preimages up to $2^n$.

"Effort" is here measured in number of invocations of the hash function on a short, "elementary" input (for SHA-256, which processes data by 512-bit block, this is the cost of processing one block).

Let's see the case for a second preimage: you have a big file $m$, that the attacker knows; the goal of the attacker is to find a $m'$, distinct from $m$, which hashes to the same value. Suppose that you used your "method 2" which splits $m$ into 32768 sub-files $m_i$, hashes each independently, then hashes the concatenated $h(m_i)$. The attacker will succeed if he finds a $m'_i$ distinct from $m_i$, but which hashes to the same value -- for any of the 32768 values of $i$. This can be called "multi-target second preimage attack". So he could try random strings until the hash of one of them matches one of the 32768 hash values $h(m_i)$. The effective cost of the attack will be $2^{n-15}$, which is less than the expected $2^n$ for a good hash function with a $n$-bit output.

(In full details, since the attacker needs his $m'_i$ to have the same length than $m_i$, he will target the SHA-256 state after the processing of the first block of each $m_i$, and use random one-block strings.)

Now do not panic, $2^{n-15}$ is still high. Indeed, it is easily seen that a successful second preimage attack necessarily implies a collision somewhere in the tree, so the resistance does not go below $2^{n/2}$, and you use a function with a 256-bit output precisely so that $2^{n/2}$ is unreachably high.

It still does not look good, in a cryptographic sense, that the tree-based hash function offers less than the theoretical maximum security that we could expect for a given output size. This can be repaired, mostly by "salting" each individual hash function invocation with the number of the sub-file it is about to process. It is not easy to get it right. In the Skein specification, as @Paŭlo describes, there is a tree-based hash method which is described; supposedly, it should avoid the issue I just detailed; however, tree-based Skein is not "the" Skein which is studied as part of the SHA-3 competition (the "SHA-3 candidate Skein" is purely sequential) and as such has not received much external scrutiny yet. Also, "the" Skein itself is still a new design and I would personally recommend against rushing things. Security is gained through old age.

As a side note, the speed advantage of Skein over SHA-256 depends on the used architecture. In particular, on 32-bit systems, Skein is slow. Recent x86 processors have a SSE2 unit which offers 64-bit computations even in 32-bit modes, so Skein is fast on any PC of the last years, provided that you use native code (C with intrinsics, or assembly). On other architectures, things are not as well; e.g., on an ARM processor (even a recent, big one, as found in a smartphone or a tablet), SHA-256 will be two to three times faster than Skein. Actually, on 32-bit MIPS and ARM platforms, and also pure Java implementations running on 32-bit x86 processors, SHA-256 turns out to be faster than all remaining SHA-3 candidates (see this report).

Answer 3

Revised: The proposed construction is just fine, and in particular:

• at least as secure as SHA-256 against collision attacks, that is the ability for an adversary to construct two files with the same hash;
• likely about as secure as SHA-256 against both first and second preimage attacks, that is the ability for an adversary to construct (for first preimage) a file with some hash given as an arbitrary value, or (for second preimage) a file with the same hash as an arbitrary given file.

The construction would slightly reduce the second-preimage resistance of a maximally resistant hash. But for SHA-256, the second-preimage resistance seems to remain no worse than allowed by a generic attack on Merkle-Damgård hashes attributed to R. D. Dean in his 1999 thesis (section 5.3.1), better exposed and refined by J. Kelsey and B. Schneier in Second Preimages on $n$-bit Hash Functions for Much Less than $2^n$ Work.

Answer 4

Method 2 is no less secure than method 1.

Here's why: the cryptographical property that a hash function possesses is that it is supposed to be computationally infeasible to find any two distinct preimages that hash to the same value. Method 1 relies on this directly. However, if we were to have an example of a collision with method 2, this implies that either:

• The inputs to the final hash differed between the two runs (and in this case, since we have an instance of two inputs leading to the exact same output, this is a collision on the underlying hash function), or

• The inputs to the final hash was exactly the same (and so, because the inputs differed somewhere, this implies that at least one of the initial hashes had differing inputs but the same output, and again, that is a collision on the underlying hash function).

In both cases, we can recover a collision, which shows both that the hash function wasn't as collision resistant as we had hoped, and also that if we were to use those two inputs as files in method 1, method 1 would also suffer a collision.

Answer 5

Is Method 2 any less secure than Method 1, in terms of collisions being more possible and/or probable?

You are just producing more values which can be used to attempt collisions, but if you pick a big enough hash space, the difference is the same as between a molecule in the ocean and a drop in the ocean.... Nothing to really worry about!

Answer 6

If a hash function is suitable for general use, it will be suitable for this use. So long as an attacker cannot find two binary strings that hash to the same value, your method is secure. If you aren't confident that's true of the hash algorithm you are using, you picked a bad algorithm.

Saying that an attacker has 32,768 opportunities to find a collision and therefore it's easier is invalid. He can just as easily try to find a collision for a single binary image by trying 32,768 different possible inputs at a time. There is no reason to expect some blocks to be stronger or weaker than others, so no reason to think more opportunities make it any easier. (Since he can replicate has single opportunity anyway.)

Answer 7

Tow methods have approximately same security. In SHA-2 and other cryptographic hash functions message break into 512-bit chunks. The good method that Paŭlo Ebermann was mentioned provide more security. there is NO known attack against Method 2 if Method 1 is secure.

EDIT: As @Pornin describes:

The effective cost of the attack will be $2^{n-15}$, which is less than the expected $2^n$ for a good hash function with a $n$-bit output.

and

The resistance does not go below $2^{\frac{n}{2}}$