Extend OTP on random data?

Question

If Alice and Bob both start with a shared OTP $P_0$, which is 256-bytes long, and Alice wants to send a 512-byte message, would it be secure to send the first 256 bytes with standard OTP ((a+b)%256 or the like), then generate another 256 bytes of true randomness ($P_1$), run that through the OTP and send the encrypted form of that. Repeat for the second block of 256 bytes and $P_1$, etc. Bob then decrypts the first 256 bytes with $P_0$ and gets $P_1$ from the second 256 bytes. Rinse and repeat, etc.

Is this secure from a passive Eve? If not, why not?

Answer 1

No, that doesn't work. OTP is secure because knowledge of the plaintext doesn't give you any useful information about the key. This is because the bits of the key (e.g. $P_0$) are never used to encrypt anything else.

If you would somehow reuse the key then leakage of the plaintext would cause leakage of $P_0$. Leakage of $P_0$ directly leaks $P_1$. I.e. instead of perfect security the information encrypted by $P_1$ is now directly dependent on the security of the plaintext and $P_0$.

OTP is only perfectly secure as long as the bits in the key stream are independent of each other. OTP doesn't allow for shortcuts in that respect.

Answer 2

If you use the OTP it has been used since its invention you will not get away with it. But there is a way that you can beat an attacker (Eve).

For the purpose of sending only text we will add a comma, full stop and a space character into an alphabet and randomise it. This will be the initial key that Alice and Bob share. The possible permutations for the randomisation are P29 = 29! = 29 x 28 x…..2 x 1. (Alphabet: P26 = 26! = 26 • 25 …….. 3 • 2 • 1 = 403,291,461,126,605,635,584,000,000)

This initial key needs to stay secret and only shared by Alice and Bob.

Below the image shows one of the possible permutations(P29); two messages we encrypted with two ciphers that displays the hex and decimal values we used to replace our text, a full stop and space characters.

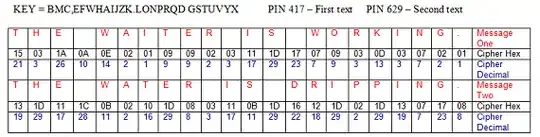
Before Alice starts to encrypt her message she creates a pin number (we used 3 digits) that will be used to create the cipher. The first step she does is moving the starting point of her first permutation by using the first number of the pin.

1. STEP = EFWHAIJZK.LONPRQD GSTUVYXBMC, Position moved by 4 (T = 21)

   Moving to the end of the string looking for the next character. When reaching the end she returns to the start of the string and moving again the position according to the next pin number.

2. STEP = FWHAIJZK.LONPRQD GSTUVYXBMC,E Position moved by 1 (H = 3, E = 26)

3. STEP = K.LONPRQD GSTUVYXBMC,EFWHAIJZ Position moved by 7 (space character = 10)

4. STEP = NPRQD GSTUVYXBMC,EFWHAIJZK.LO Position moved by 4

5. STEP = PRQD GSTUVYXBMC,EFWHAIJZK.LON Position moved by 1

6. STEP = TUVYXBMC,EFWHAIJZK.LONPRQD GS Position moved by 7

7. STEP = XBMC,EFWHAIJZK.LONPRQD GSTUVY Position moved by 4

8. STEP = BMC,EFWHAIJZK.LONPRQD GSTUVYX Position moved by 1

9. STEP = HAIJZK.LONPRQD GSTUVYXBMC,EFW Position moved by 7

10. Step = ZK.LONPRQD GSTUVYXBMC,EFWHAIJ Position moved by 4 (full stop = 1)

What Alice did is creating a string of random numbers which are as random as characters picked by an operator. Each number can represent any of the 29 characters in our randomised extended alphabet (1/29). Linguists too will have a problem to identify pattern that language holds since the randomization of our extended alphabet has destroyed them; and recording differences between characters doesn’t give anything away about the frequency of characters.

Now Alice can email her message and the pin code (of no use to an attacker without the correct permutation) and Bob can reverse it by using the pin code.

For a system that can encrypt text (no restrictions on languages), images, media files etc use a randomized ASCII (extended 256).