Ciphertext-only attacks on randomly permuted many-time-pad

Question

Consider the encryption scheme where an $n$-bit message $m$ is encrypted with an $n$-bit key $k$ by randomly choosing a permutation $\pi$ of $1,2,3,\dots,n$, and the ciphertext is the pair $(\pi, \pi(m) \oplus k)$ (where $\pi(m)$ is the bits of $m$ permuted according to $\pi$). Are there any known ciphertext-only attacks on this scheme, assuming the distribution of $m$ is English text? None of the approaches I know of, e.g. crib dragging, seem applicable in this case.

Answer 1

It's easier to break than many-time-pad without permutation

The scheme is quite easy to break if something is known about the input bit probabilities. For example, ASCII text characters usually have top bit of each byte unset. Because of the permutation it will land on different bits, and because we know where it lands, we then know that bit of the pad. Without the permutation, at least the known probability bits would be aligned, which would give us less information.

With the assumption of English text, we can further refine the bit probabilities.

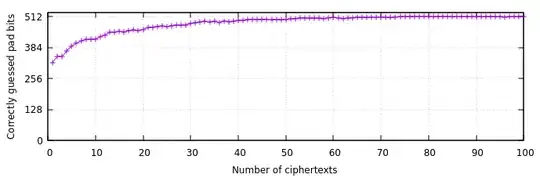
For the fun of it, I simulated this using Python with the following assumptions:

• English uppercase letters with typical letter frequency
• Message length 64 characters (512 bits)
• A set of 1 to 100 ciphertexts used for guessing

In this case we know from the upper case letters that the top bits are always '010', and can estimate the probability of the lower bits. At random chance, you would expect half of the bits to be guessed correctly.

Already at 50 ciphertexts, the pad is mostly broken. If the text was using the whole 7-bit ASCII character set, it takes around 200 ciphertexts of this length to break it.

Because of the bit-to-bit correspondence, even partially erroneous pad is enough to guess the message content. For example, after only 30 ciphertexts a message of ATTACK AT DAWN can be decoded as ApTE?K @T D?WN.

Here is the code used for the simulation:

import random
letter_freq = {'E': 13, 'T': 9, 'A': 8, 'O': 8, 'I': 7, 'N': 7, 'S': 6, 'H': 6, 'R': 6, 'D': 4, 'L': 4, 'C': 3, 'U': 3, 'M': 2, 'W': 2, 'F': 2, 'G': 2, 'Y': 2, 'P': 2, 'B': 1, 'V': 1, 'K': 1, 'J': 1, 'X': 1, 'Q': 1, 'Z': 1}
msglen = 64
bitcount = msglen * 8
def get_msg():
    '''Pick random letters to form a message'''
    return random.sample(list(letter_freq.keys()), msglen, counts = list(letter_freq.values()))
def encrypt(msg, pad):
    '''Permute the message and XOR with pad'''
    bits = ''.join(format(ord(x), '08b') for x in msg)
    permutation = list(range(bitcount))
    random.shuffle(permutation)
    encrypted = ''.join(format(bits[permutation[i]] != pad[i], '01d') for i in range(bitcount))
    return (tuple(permutation), encrypted)
def decrypt(ciphertext, pad):
    '''Decrypt a message back to string'''
    permutation, bitstring = ciphertext
    result = [0] * msglen
    for i in range(bitcount):
        if bitstring[i] != pad[i]:
            bitpos = permutation[i]
            result[bitpos // 8] |= (0x80 >> (bitpos % 8))
return ''.join((chr(b) if b > 20 and b < 128 else '?') for b in result)


def get_bit_probability():
    '''Get probability of each bit being set in English text'''
    probs = [0] * 8
    for i in range(8):
        for c, f in letter_freq.items():
            if ord(c) & (1 << i):
                probs[i] += f
    return probs
def guess_pad(ciphertexts):
    '''Calculate probabilities for each bit in pad'''
    bit_probs = get_bit_probability()
    key_probs = [0] * bitcount
    for ciphertext in ciphertexts:
        permutation, bitstring = ciphertext
        for i, bitval in enumerate(bitstring):
            sign = (1 if bitval == '1' else -1)
            key_probs[i] += bit_probs[permutation[i] % 8] * sign
return ''.join(format(k &gt; 0, '01d') for k in key_probs)


Generate random pad of msglen bytes, and convert to bitstring
secret_pad = ''.join([format(x, '08b') for x in random.randbytes(msglen)])
example_ciphertext = encrypt("ATTACK AT DAWN".ljust(msglen), secret_pad)
ciphertexts = []
print("# Message count,  Bits correct, Example decoded message")
for i in range(100):
    ciphertexts.append(encrypt(get_msg(), secret_pad))
    guessed_pad = guess_pad(ciphertexts)
    bits = sum(guessed_pad[i] == secret_pad[i] for i in range(bitcount))
print(len(ciphertexts), bits, decrypt(example_ciphertext, guessed_pad))

Answer 2

There's a simple attack if we assume many ciphertexts, and the distribution of bits in multiple messages is biased, e.g. towards 0. Each bit of key at a given position is likely to be the most common value in ciphertext at this position.

Answer 3

Everybody who has read Shannon’s papers knows that in his proof perfect secrecy is achieved by having a unique key character for each plaintext character. But this also implies that the plaintext is a property that in his own right can be measured.

Change that and the key is not important anymore (key length becomes irrelevant). ————- Since I’m new on this board I have no privileges to answer your call for clarification (Command Master). I’m doing that on Reddit where I found more sensible people. Two down votes here already convinces me that I’m not dealing with logical thinking people here. And requiring privileges to have a sensible discussion is a joke, isn’t it? The math professors at universities and 6 AI systems confirming our mathematical conclusions can’t be wrong. The two people voting my comment down in comparison are fitting in here. I’m not, because I take science seriously.